Kirigami takes pop-up books to a whole new level. The Japanese paper craft involves cutting patterns in paper to transform a two-dimensional sheet into an intricate, three-dimensional structure when partially folded. In the hands of an artist, kirigami can yield remarkably detailed and delicate replicas of structures in nature, architecture, and more.
Scientists and engineers have also taken inspiration from kirigami, applying principles from paper-cutting to design robotic grippers, stretchable electronics, water-harvesting sheets, and other shape-shifting materials and devices. For the most part, such inventions are products of from-scratch design. There’s been no blueprint for engineers to determine the pattern of cuts that will transform a material from one desired shape to another — that is, until now.
A new study in Nature Computational Science presents a general computational strategy that can solve any two-dimensional, kirigami-inspired transformation. The method can be used to determine the angle and length of cuts to make, such that a sheet can transform from one desired shape to another when pulled open and pushed back together, like an intricate, expandable lattice.
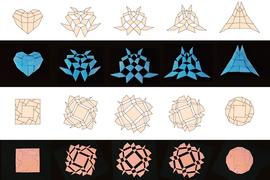
With their new method, researchers designed and fabricated a number of transformable, 2D kirigami structures, including a circle that turns into a square, and a triangle that morphs into a heart.

“People have talked of the square and circle as one of the impossible problems in mathematics: You cannot turn one into the other,” says Gary Choi, a postdoc and instructor in applied mathematics at MIT. “But with kirigami, we can actually turn a square shape into a circle shape.”
For engineers, the new method could be used to solve various design problems, such as how a robot can be engineered to transform from one shape to another to carry out a particular task or navigate certain spaces. There’s also potential to design active materials, for instance as smart coverings for buildings and homes.
“One of the first applications we thought of was building façades,” says Kaitlyn Becker, an assistant professor of mechanical engineering at MIT. “This could help us to make large, kirigami-like façades that can transform their shape to control sunlight, ultraviolet radiation, and be adaptive to their environment.”
Becker and Choi are co-authors of the new study, along with Levi Dudte, a quantitative researcher at Optiver, and L. Mahadevan, a professor at Harvard University.
The space between
The study grew out of the team’s previous work in both kirigami and origami — the Japanese art of paper folding.
“We found there are a lot of mathematical connections in kirigami and origami,” Choi says. “So we wanted to come up with a mathematical formulation that can help people design a large variety of patterns.”
In 2019, the team devised an optimization approach for kirigami to find the pattern of cuts that would be required to turn one shape into another. But Choi says the approach was too computationally intensive, and it took a large amount of time to derive an optimal pattern to achieve a particular transformation.
In 2021, the researchers took on a similar problem in origami and found that through a slightly different perspective, they were able to derive a more efficient strategy. Rather than planning out a pattern of individual folds (similar to kirigami’s individual cuts), the team focused on growing a pattern from a simple folded seed. By working panel by panel, and establishing relationships between panels, such as how one panel would move if an adjacent panel were folded, they were able to derive a relatively efficient algorithm for planning out the design of any origami structure.
The team wondered if a similar approach be applied to kirigami. In traditional kirigami, once cuts have been made in a sheet of paper, the sheet can be partially folded such that the resulting empty spaces create a three-dimensional structure. Like the panels between origami folds, could the empty spaces between cuts, and their relation to each other, yield a more efficient formula for kirigami design? This question motivated the team’s new study.
Math links
The study focuses on two-dimensional kirigami transformations. The researchers considered a general kirigami design comprising a mosaic of interconnected quadrilateral tiles, each cut to various angles and sizes. The conceptual mosaic begins as one shape and can be pulled apart and pushed back together to form an entirely new shape. The challenge was to describe how one shape can transform into another, based on the empty spaces between tiles and how the spaces change as the tiles are pulled apart and pushed back together.
“If the tiles themselves are solid and unchangeable, then it’s the empty spaces between that are an opportunity for motion,” Becker says.
The team first considered the simplest representation of empty space, in the form of a rhombus, or what they term a “four-bar linkage.” Each side of the rhombus represents a bar, or the edge of a solid tile. Each corner of the rhombus represents a linkage, or hinge that connects tiles. By changing the length and angle of the rhombus’ edges, the team could study how the empty space in between changes.
By studying progressively larger assemblages of four-bar linkages, the team identified relationships between the angle and length of bars, the shape of individual empty spaces, and the shape of the overall assemblage. They worked these relationships into a general formula, and found that it could efficiently identify the pattern of cuts — including their angle and length — that would be required to transform a two-dimensional sheet from one desired shape to another.
“Without a tool like this, I might brute force this problem in Matlab, or guess and check, but it would take me a very long time to get something that can transform from a circle to a square,” Becker says.
In simulations, the team found that the formula could indeed find a pattern of tiles that would turn a circle-shaped mosaic into a square, as well as virtually any shape into any other desired shape.
Going a step further, the team developed two fabrication methods to physically realize the formula’s designs. They quickly realized that a key challenge in making the transformable mosaics was in finding the right material to serve as the tile-connecting hinges. The connections needed to be strong, yet easily bendable.
“I thought, what is very strong in tension, and tear-resistant, but can have a zero bending radius, almost like a pinpoint hinge?” Becker says. “And the answer, it turns out, is fabric.”
The team used two methods — 3D printing, and mold casting — to embed small strips of fabric into quadrilateral plastic tiles, in a way that closely connected the tiles while allowing them to bend against each other. Using these two methods, the team fabricated circle-shaped mosaics that transformed into squares, as well as simple triangle mosaics that morphed into more complex heart shapes.
“We can basically go to any two-dimensional shape,” Choi says. “That’s guaranteed, using our mathematical formulation. Now we’re looking to extend this to 3D kirigami.”